Tree

A tree is a non-linear data structure where each node is connected to a number of nodes with the help of pointers or reference.

Binary tree

A tree is said to be a binary tree if all of its nodes have atmost 2 children.

Properties of Binary Tree

In a binary tree, level n can have up to 2n nodes.
There can be a maximum of 2^h-1 nodes in a binary tree of height h.
In a binary tree with N nodes, the minimum possible height or minimum number of levels is log2(N+1).

Types of Binary Tree

Full Binary tree : A binary tree is full if every node has either 0 or 2 children.
Complete Binary tree : A binary tree is complete if all the levels are completely filled except possibly the last.
Perfect Binary tree : A binary tree is a perfect tree when all internal nodes have two children and all the leave nodes are at the same level.

Applications of trees

Trees are used to store information that naturally forms a hierarchy. For example, the file systems on a computer.
Store hierarchical data, like folder structure, organization structure, XML/HTML data.
Binary Search Tree is a tree that allows fast search, insert, delete on a sorted data. It also allows finding closest item.

Representation of Binary Tree

Each node contains the following:

Data
Pointer to the left child
Pointer to the right child

Class Node{
public:
   int data;
   Node* left;
   Node* right;

   // Constructor
    Node(int val) {
    data=val;
    left=right=NULL:
}
};
int main(){

Node* root = new Node(1);
root->left=new Node(2);
root->right=new Node(3);
return 0;
}

Binary Tree Traversals

In tree we have different ways in which we traverse nodes.

There are two types of traversing:

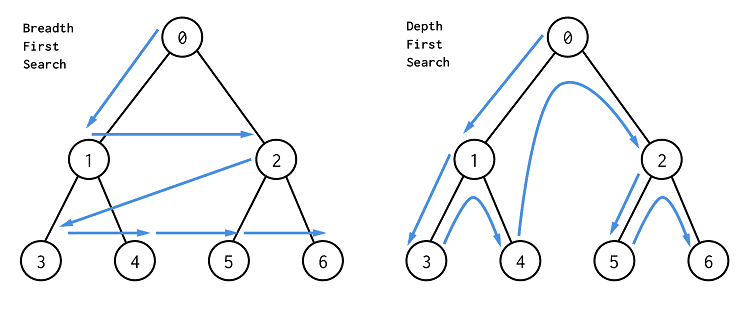
BFS vs DFS Algorithms

BFS stands for Breadth First Search. It is also known as level order traversal. The Queue data structure is used for the Breadth First Search traversal. When we use the BFS algorithm for the traversal in a graph, we can consider any node as a root node.
DFS stands for Depth First Search. In DFS traversal, the stack data structure is used, which works on the LIFO (Last In First Out) principle. In DFS, traversing can be started from any node, or we can say that any node can be considered as a root node until the root node is not mentioned in the problem.

In this we have these three traversal mentioned below

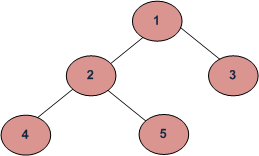
Example Tree

Inorder (Left, root, right) : 4,2,5,1,3
Preorder (Root, left, right) : 1,2,4,5,3
Postorder (Left, right, root) : 4,5,2,3,1

Now lets dive deep into these

Inorder Traversals : In Inorder traversal, a node is processed after processing all the nodes in its left subtree. The right subtree of the node is processed after processing the node itself.

Algorithm for inorder:
1. Inorder(root->left)
2. Visit node
3. Inorder(root->right)
Preorder Traversal : In preorder a node is processed before processing any of the nodes in its subtree

Algorithm preorder:
1. Visit the node
2. Preorder(root->left)
3. Preorder(root->right)
Postorder Traversal : In Postorder a node is processed after processing all the nodes of its subtree

Algorithm postorder:
1. Postorder(root->left)
2. Postorder(root->right)
3. Visit the node

Now some for the questions on Binary tree

Height of Binary Tree

In this we assume root node at level 1.

int height(Node* root)
{
 if(root==NULL)
    return 0;
 else
    return(max(height(root->left),height(root->right))+1);
}

Print the nodes at kth level

I we assume root node at distance 0.

void printkthnode(Node* root,int k){
if(!root || k<0){
return;
}

    if(k==0)
        cout<<root->data;
    else
        printkthnode(root->left,k-1);
        printkthnode(root->right,k-1);

}

Level order traversing or BFS

In this we use queue data structure, we push root element an then we loop until queue gets empty, in each iteration we process the node and if there left and right present we push them in queue.

// Level order traversing or BFS

void bfs(Node* root){
    if(!root) return;

    queue<Node*> q;

    q.push(root);
while(!q.empty()){
  Node* node=q.front();
    q.pop();
    cout<<q->data;

    if(node->left) q.push(node->left);

    if(node->right) q.push(node->right);
    }
}

In above we get all the elements in bfs form but in single array, If we wish to have 2d array with each level as an element of 2-d array, we have to use a for-loop inside while-loop.

vector<vector<int>> bfs(Node* root){

    vector<vector<int>> ans;
        if(!root) return ans;
     queue<Node *> q;
    q.push(root);
    while(!q.empty()){
    int size=q.size();
    vector<int> level;
    for(int i=0;i<size;i++){
        Node * temp=q.front();
          q.pop();

           level.push_back(temp->data);
        if(temp->left) q.push(temp->left);
         if(temp->right) q.push(temp->right);
            }
        ans.push_back(level);
    }
return ans;
}

Tree | Binary tree (Part - 1)